
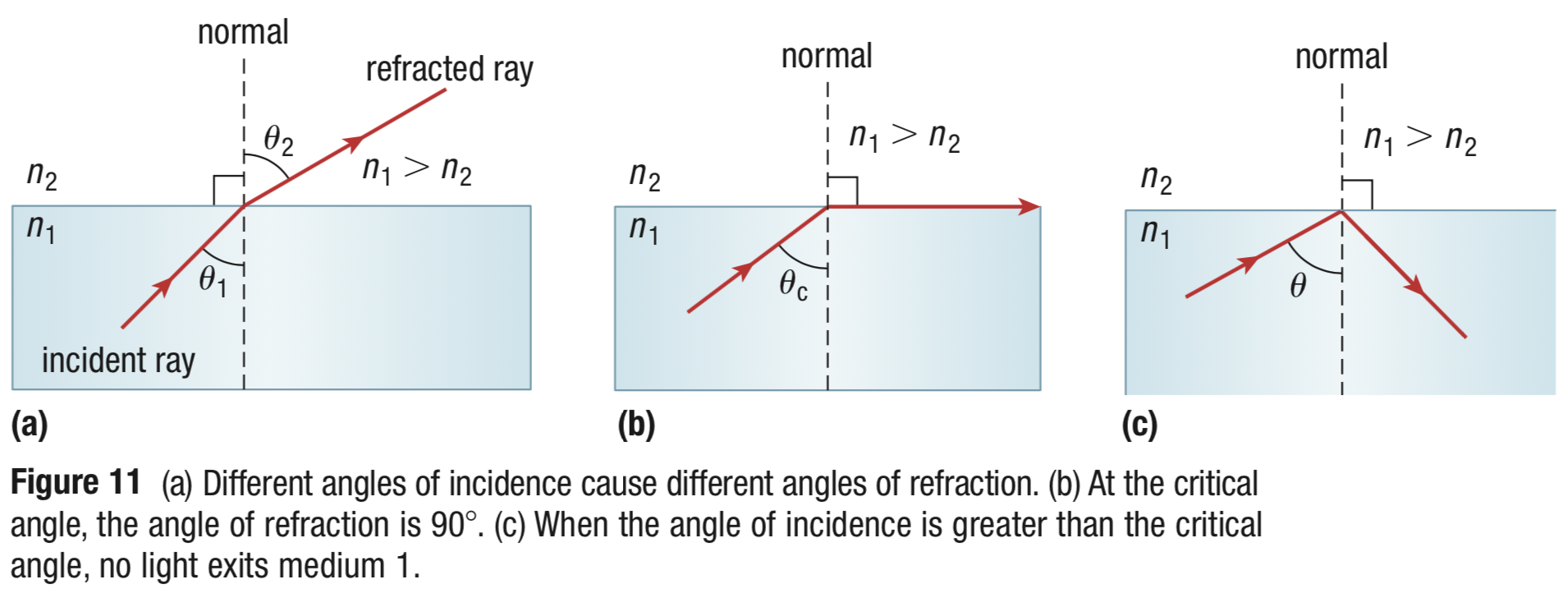
Optical fibres or fibre optics have applications in a variety of fields, such as communications to transmit telephone signals, cable TV signals, the internet, and medical signals. Total Internal Reflection In Optical Fiber - Key takeaways Total internal reflection is a phenomenon of light that occurs when the angle between the incident light and the normal of the boundary θ1 is greater than the critical angle θc.An optical fibre is a nonconducting waveguide that transmits light along its axis by total internal reflection. These fibres are very thin, which allows light to enter from one side and strike the inside of the fibre with an angle greater than the critical angle, which causes them to travel through the fibre and exit it at the same angle as the entry angle.Ĭladding is the coating outside of optical fibres that have a refractive index that is smaller than the material inside the optical fibre and thus prevents light from being refracted between the fibres in a bundle.Ī light beam travelling through an optical fibre Optical fibres or fibre optics have applications in a variety of fields, such as communications to transmit telephone signals, cable signals, TV signals, the internet, and medical signals. This is related to Total Internal Reflection in Optical Fibre. We should note that two conditions need to be fulfilled for total internal reflection of light to occur: (1) the incident angle must be greater than the critical angle (θ1 > θc), and (2) the refractive index of the initial medium must be greater than the refractive index of the second medium (n1 > n2). Therefore, the critical angle between the boundaries of two materials where n1 > n2 can be determined using the following equation: When the incident angle equals the critical angle, or θ1 = θc, the refraction angle is 90° and sin90° = 1. According to Snell's law, the ratio of the sines of the incident and refraction angles is constant between two mediums. As the incident angle θ1 increases, so does the refraction angle θ2, but it can only go up to 90° when the incident angle equals the critical angle θc (Figure 1 (b)). The refraction angle θ2 is greater than the incident angle θ1 because the refractive index of the second boundary n2 is less than the refractive index of the first boundary. When we use mirrors in our daily lives, they reflect about 90% of the light and absorb the remaining portion, which is refracted as shown in Figure 1 (a). The behaviour of a light beam related to the refractive index and the angle of incidence


 0 kommentar(er)
0 kommentar(er)
